12/Oct/08

Revista Axxón Axxón en facebook Lectores de Axxón en facebook

Haciendo ondas

En un seminario organizado en colaboración por la Stanford University y el American Institute of Mathematics, Soundararajan anunció que él y Roman Holowinsky habían demostrado una significativa versión de la conjetura de única ergodicidad (QUE)

"Éste es uno de los mejores teoremas del año", dijo Peter Sarnak, matemático de Princeton quien con Zeev Rudnick de la Universidad de Tel Aviv formularon la conjetura hace quince años, en un esfuerzo por comprender las conexiones entre la física clásica y la cuántica. "Sabía que Soundararajan y Holowinsky estaban atacando QUE usando técnicas diferentes y quedé asombrado al descubrir que sus métodos se combinaban milagrosamente para resolver el problema completamente", dijo Sarnak. Ambos enfoques vienen de la teoría del número, un área de la matemática pura que recientemente ha probado tener sorprendentes conexiones con la física.

La motivación detrás del problema es comprender cómo las ondas son influidas por la geometría de su continente. Imagine ondas de sonido en una sala de conciertos. En una sala de conciertos bien diseñada se puede escuchar cada nota desde cada asiento. Las ondas de sonido se esparcen de manera uniforme y pareja. En el extremo opuesto están las "galerías susurrantes" donde el sonido se concentra en una área pequeña.

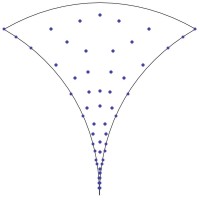Puntos distribuidos
uniformemente en un
dominio fundamental para SL (2, Z).

El mundo matemático está habitado por toda clase de formas, algunas de las cuales son fáciles de describir, como las esferas y las rosquillas, y otras que son construidas desde la matemática abstracta. Todas estas formas tienen ondas asociadas. Soundararajan y Holowinsky mostraban que para ciertas formas que vienen de la teoría del número, las ondas siempre se dispersan de manera pareja. Para estas formas no hay ninguna "galería susurrante".

Caos cuántico

La conjetura cuántica de única ergodicidad (QUE) viene del área de la física conocida como "caos cuántico". El objetivo del caos cuántico es comprender la relación entre la física clásica -las reglas que gobiernan el movimiento de objetos macroscópicos como personas y planetas, cuando su movimiento es caótico- con la física cuántica -las reglas que gobiernan el mundo microscópico.

"El trabajo de Holowinsky y Soundararajan es brillante", dice el físico Jens Marklof de la Universidad de Bristol, "y nos cuenta sobre el comportamiento de una partícula atrapada sobre la superficie modular en un poderoso campo magnético".

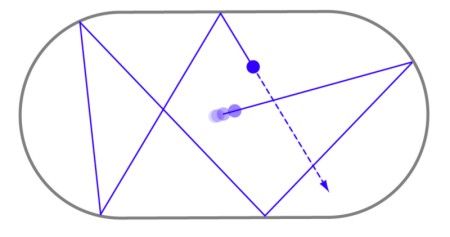
Los problemas del caos cuántico pueden ser comprendidos en términos de billares. En una mesa estándar de billar -rectangular- el movimiento de las pelotas es predecible y fácil de describir. Las cosas se ponen más interesantes si la mesa tiene bordes curvos, conocida un "estadio". Entonces resulta que la mayor parte de las trayectorias son caóticas y con el tiempo llenan la mesa de billar, un resultado demostrado por el físico matemático Leonid Bunimovich.

En un marco cuántico o microscópico, uno investiga las ondas que están asociadas a la mesa de billar. A menudo las ondas se dispersan de manera uniforme. A veces, sin embargo, las ondas se concentran a lo largo de una trayectoria periódica inestable, como se muestra en la imagen arriba. Los físicos llaman esto "cicatriz".

Para el sistema estadio, otra cosa interesante puede ocurrir, conocida como "modo de rebote de pelota". Los modos de rebote de pelota fueron observados experimentalmente y sólo recientemente Andrew Hassell demostró que existían.

En su conjetura QUE, Rudnick y Sarnak plantearon la hipótesis de que para una gran clase de sistemas, a diferencia del estadio, no hay cicatriz ni estados de rebotes de pelota, y que de hecho todos los estados se vuelven uniformemente distribuidos. El trabajo de Holowinsky y Soundararajan muestra que la conjetura es verdad en el marco teórico del número.

Estados muy excitados

Soundararajan, Stanford University

La conjetura de Rudnick y Sarnak trata ciertas clases de formas llamadas colectoras, o más técnicamente, colectoras de curvatura negativa, algunas de las cuales vienen de problemas en alta aritmética. Las ondas correspondientes son análogas a los estados altamente excitados en la mecánica cuántica.

Roman Holowinsky, University of Toronto.

Soundararajan y Holowinsky desarrollaron nuevas técnica para resolver un particular caso de Que. Las "ondas" en este marco son conocidas como eigenformas Hecke holomórficas. Los enfoques de ambos investigadores funcionan por separado la mayor parte del tiempo y cuando los combinan resuelven milagrosamente el problema completo. "Su trabajo es una encantadora mezcla de ideas de la física y de la matemática abstracta", dijo Brian Conrey, director del American Institute of Mathematics.

De acuerdo con Lev Kaplan, físico en la Tulane University: "Es un buen ejemplo de trabajo matemático inspirado por un interesante problema físico, y tiene relevancia en nuestra comprensión del comportamiento cuántico en sistemas clásicos de dinámica caótica".

Fuente: AiMath. Aportado por Graciela Lorenzo Tillard