20/Ago/07

Revista Axxón Axxón en facebook Lectores de Axxón en facebook

La luna Atlas de Saturno: ¿una "duna" voladora?

El modelo que aquí presentamos elabora un teoría sobre la forma de Atlas. El mismo surgió como consecuencia de las distintas opiniones expresadas en un foro de astronomía de la página web: www.sondasespaciales.com.

El 12 de junio de 2007 la sonda Cassini envió las imágenes de un pequeño satélite de Saturno llamado Atlas que se sitúa entre el anillo A y el pequeño anillo R/2004 S 1. Estas imágenes han mostrado que la morfología de Atlas es muy diferente a las de otros satélites de dimensiones similares. En el presente artículo se propone una teoría plausible, a la que denominamos "duna voladora", que explica sus características morfológicas a partir de sus magnitudes como masa, diámetros y radio orbital, así como por su posición orbital y la interpretación de las imágenes captadas por la sonda Cassini.

Introducción.

En 1980 la sonda Voyager 1 sobrevoló Saturno enviando fotografías del planeta, sus anillos y satélites. Richard J. Terrile, en octubre de 1980 descubrió en estas fotografías una nueva luna que orbitaba ligeramente exterior al anillo A, a la que llamó provisionalmente 1980 S28. Más adelante se le pondría el nombre definitivo de Atlas.

El 8 de junio de 2005 la sonda Cassini se acercó a Atlas a una distancia de 428.551 km obteniendo distintas fotografías que mostraban un satélite con una fuerte simetría en su eje polar. Una ampliación de esta fotografía del 2005 nos revela que la morfología del satélite tiene forma de disco:

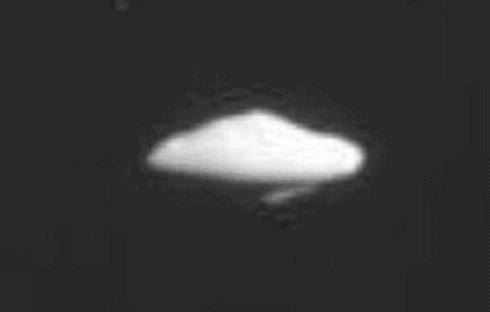
El 12 de junio de 2007 Cassini obtiene una serie de imágenes de mejor resolución de Atlas vista desde el plano polar:

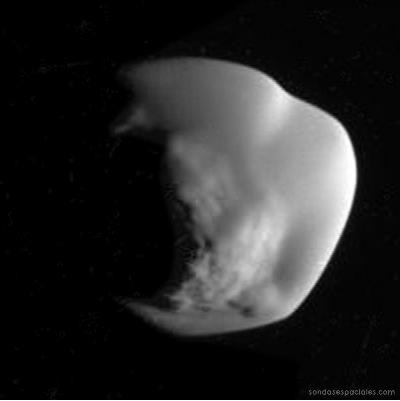
Si comparamos las imagenes de Atlas del 8 de octubre de 2005 y 12 de junio de 2007 con las imágenes que tenemos de otros satélites "pequeños" de Saturno, encontramos varias notables diferencias.

Se aprecia que las diferencias entre Atlas y otros satélites del sistema solar -como Prometheus, Pandora y Epimeteo (satélites de Saturno) de órbitas cercanas y tamaños ligeramente superiores, o Amaltea y Thebe (satélites de Júpiter) también de parámetros muy similares o Phobos y Deimos (satélites de Marte) cuyas masas son menores que las de Atlas- son las siguientes:

• Todos los satélites son irregulares mientras que la forma de Atlas tiene un eje de simetría central perpendicular al plano de rotación y del anillo de Saturno.

• El resto de satélites muestran marcas de cráteres de las que carece Atlas.

• Las superficies de los demás satélites asemejan rocas de aspecto áspero, mientras que la superficie de Atlas parece pulida.

El límite de Roche y Atlas.

El "límite de Roche" es la distancia a la cual un satélite cuya estructura se mantiene cohesionada únicamente por su propia gravedad comienza a disgregarse debido a que las fuerzas de marea gravitatoria del planeta al que orbita y a la fuerza centrípeta de su rotación son mayores que su fuerza gravitatoria de cohesión.

Existen dos ecuaciones distintas para calcular este límite según el satélite sea rígido o deformable. La diferencia entre ambas ecuaciones depende solo de un parámetro. Nuestro objetivo será conocer cual es el valor del limite de Roche para el satélite Atlas tanto si consideramos que se trata de un satélite rígido o de uno deformable. Para ello deberemos conocer el valor de la masa del satélite.

Lamentablemente no conocemos el valor de la masa de Atlas con suficiente precisión. Según la fuente que consultemos encontramos valores como 8•10¹⁷ kg (sse.jlp.nasa,gov), 2•10¹⁵ kg (saturn.jpl.nasa.gov) o 6,59•10¹⁵ kg (Spitale, J. N.; Jacobson, R. A.; Porco, C. C.; Owen, W. M., Jr.). Esta diversidad de datos nos impide conocer si Atlas está dentro o fuera del límite de Roche para un cuerpo sólido.

Sin embargo, incluso con el mayor valor de masa para Atlas, este siempre está dentro de su límite de Roché para un satélite deformable. Es decir, Atlas no puede ser "simplemente" un objeto deformable.

Propuesta sobre la naturaleza de Atlas.

Con los datos obtenidos, Atlas no puede ser un satélite deformable, pero vistas sus imágenes (sin cráteres y con simetría en el eje de rotación) tampoco puede tratarse de un satélite rígido como Pandora, Thebe o Phobos.

En consecuencia, la única opción que hace compatible las observaciones y los cálculos de los Límites de Roche es que Atlas sea un objeto en parte sólido y en parte deformable tal como un núcleo rocoso recubierto de una capa de polvo. Al ser el núcleo rígido la deformación del satélite no es completa como si fuera todo él deformable. Utilizando los datos de Spitae, la masa rígida debe rondar el 43% y la deformable el 57%.

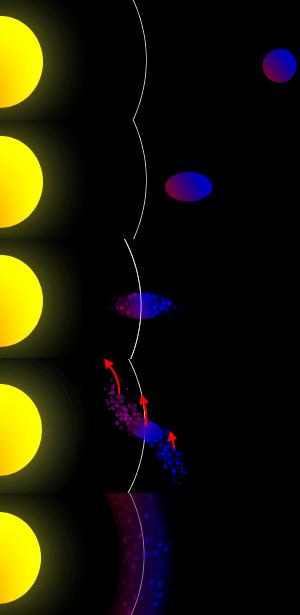
Puesto que la condición de estabilidad gravitatoria para un objeto así sería la de un núcleo central de roca rodeado de una nube de polvo en forma de duna, este modelo bien puede ser bautizado como "duna voladora" (ver figura 1).

En base al estudio de este campo gravitatorio y al análisis de fuerzas que concurren en Atlas, se puede establecer un modelo matemático cuya ecuación consta de dos partes: una parte ovoidal de estabilidad gravitatoria (circum) y otra parabólica de inestabilidad (f(x)) cuya localización supone una órbita en torno a Saturno. Las posiciones de estas dos curvas dependen de parámetros tales como la masa y densidad de las distintas partes de Atlas.

En resumen, las ecuaciones de Atlas permiten determinar el ovoide de estabilidad gravitatoria y un lugar de inestabilidad que se movería en torno a Saturno. Según la excentricidad de la órbita de Atlas o la cantidad de polvo que capturara, se podría producir con facilidad este intercambio de materia.

Sorprendentemente, a 40 km de Atlas se encuentra el pequeño anillo R/2004 S 1.

Es decir, con el modelo no solo describo al satélite si no también al anillo. Dicho de otra forma, satélite y anillo están ligados por la misma familia de ecuaciones. Ambos comparten el mismo polvo anular y por ello Atlas, en vez de ser una roca, como los demás asteroides, tiene una duna de polvo en su plano ecuatorial. El polvo de Atlas y el del anillo R/2004 S 1 son lo mismo, ligado mediante las mismas ecuaciones.

Representación gráfica de Atlas.

El resultado de aplicar las ecuaciones a Atlas es:

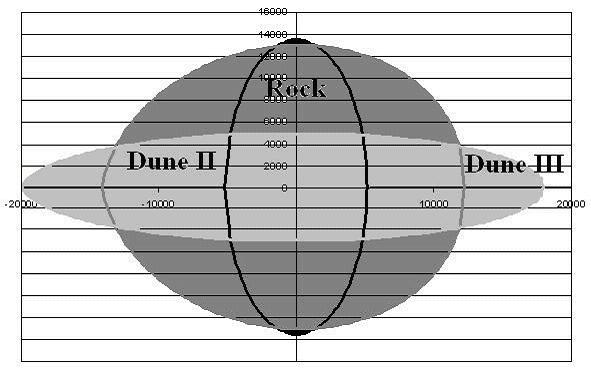
En buena consonancia con las imágenes tomadas por la sonda Cassini (ver arriba).

Fuente: Sondas Espaciales. Aportado por Francisco Costantini