El primer encuentro de Ug con las estrellas
Tratemos de imaginar a uno de nuestros antepasados, el primero que adquirió conciencia de sí mismo. Llamémosle, por cortedad, Ug. Ug, luego de maravillarse de sí mismo, de lo que camina por la tierra, de lo que nada en el mar y en los ríos y lagos y de
lo que vuela por los aires, levanta la mirada al cielo. Lo que ve lo asombra. Una gran bola amarilla, brillante y caliente, que recorre la bóveda celeste y se oculta tras el horizonte. Cuando esta bola radiante desaparece, se apersona el frío y aparecen
multitud de puntitos brillantes sobre un telón negro. No es difícil imaginar lo sobrecogedor que esto debe haber sido para Ug. La primera vez que vio este fenómeno habrá pensado que su vida tocaba a su fin, o quizá algo peor, hasta que el Sol volvió a aparecer en el cielo. A partir de entonces Ug debe haber notado el ciclo día-noche que marca en inicio de la curiosidad astronómica.
A medida que pasaron las generaciones, los hombres pasaron del ciclo día-noche al ciclo estacional, que les era vital para sobrevivir, tanto si dependían de la caza como si dependían de la siembra. Y con el tiempo aparecieron los pensadores, esos extraños
seres que se hacían preguntas que no tenían relación directa con la supervivencia de la especie. Hacia el siglo IV antes de Cristo, la creencia generalizada era que la Tierra era un cuerpo inmóvil alrededor del cual giraban los astros. Y era lo más natural.
¿Acaso nosotros vemos que nuestra Tierra, la que tenemos bajo los pies, se está moviendo? Claro que no. Pero sí vemos que el Sol y las estrellas lo hacen. En esta época apareció un visionario, Aristarco de Samos, quien pensaba que la Tierra giraba sobre
su eje una vez al día, y que junto con los demás astros giraba alrededor del Sol. Semejante absurdo no fue aceptado por ninguna persona medianamente razonable. Así que la Tierra siguió inmóvil. A esta idea la llamamos Sistema Geocéntrico.
Dos siglos después, en Grecia, Hiparco de Nicea y Ptolomeo determinaron las posiciones relativas de unas mil estrellas con respecto a la Tierra, y midieron su movimiento. Con los resultados de sus mediciones, Ptolomeo concluyó que los objetos celestes
giraban en torno a la Tierra y planteó un modelo de universo con la Tierra en el centro. Cada cuerpo celeste se trasladaba por una órbita circular llamada epiciclo, cuyo centro se movía a su vez alrededor de la Tierra en una trayectoria circular llamada
deferente.
El modelo ptolemaico se mantuvo vigente por mucho tiempo. Sólo en el siglo XVI, Nicolás Copérnico revisó el modelo de Ptolomeo y demostró que los movimientos de los astros podían explicarse con un universo en el cual el Sol ocupara la posición central.
Copérnico publicó sus ideas en 1543, en una obra titulada "De revolutionibus orbium caelestium", dando origen al Sistema Heliocéntrico. Posteriormente, el italiano Galileo Galilei aportó pruebas para defender las hipótesis de Copérnico. Una de ellas fue
la observación de cuatro lunas que giraban alrededor de Júpiter, con un telescopio de refracción (con una lente en vez de un espejo) que construyó él mismo en 1609. Es común en la ciencia refutar un modelo a través de lo que se llama un contraejemplo,
es decir, un ejemplo que contradice al modelo. Galileo observó que las lunas de Júpiter giraban alrededor de Júpiter, y no de la Tierra, por lo cual, al existir al menos un objeto celeste que no cumplía el modelo ptolemaico, tal modelo no era correcto,
al menos no completamente. Aunque la Iglesia logró que Galileo renegara de sus ideas, éstas no pudieron ser completamente suprimidas.
2
"... y sin embargo se mueve"
En este punto, los modelos que se habían formulado no eran predictivos, es decir, no podían usarse para predecir el comportamiento de los astros. El alemán Johannes Kepler cambió esto al formular las leyes del movimiento planetario, la famosas leyes de
Kepler, basándose en las observaciones que hizo su colega danés Tycho Brahe hacia finales del siglo XVI de los movimientos del Sol, la Luna y los planetas.
En lenguaje simple las leyes de Kepler son las siguientes:
1- Los planetas describen órbitas elípticas alrededor del Sol. El Sol se encuentra en uno de los puntos focales de la elipse. Una elipse es una curva cerrada ovalada, que se caracteriza por tener un semieje mayor y un semieje menor, cuyos tamaños se relacionan
entre sí según la distancia entre el punto focal y el centro de la elipse. Un círculo es una elipse especial cuyos semiejes son iguales, y el punto focal está en el centro. Para los que les gustan las ecuaciones, sea a el semieje mayor de la elipse, b
el semieje menor y c la distancia focal, entonces la elipse cumple con la siguiente ecuación: a2 = b2 + c2. Observemos que, si a = b (los dos semiejes son iguales, el caso del círculo), se cumple que c = 0, es decir, el foco
está sobre el centro del círculo.
2- El vector posición de un planeta (la línea que une al planeta con el Sol) barre áreas iguales en periodos de tiempo iguales. Esto quiere decir que el planeta se moverá más rápido cuanto más cerca esté del Sol, y más lento a medida que se aleje del Sol.
El planeta se mueve con su máxima velocidad cuando está en el punto más cercano al Sol, llamado perihelio, y a su mínima velocidad en el punto más lejano (afelio). En ecuaciones, esto equivale a decir que d1 . v1= d2 . v2, siendo d1 la distancia del planeta al Sol en el punto 1 de su órbita, v1 la velocidad que tiene al pasar por el punto 1, d2 la distancia del planeta al Sol en el punto 2 de su órbita, y v2 la velocidad que tiene al pasar por el punto 2.
3- El periodo de revolución de un planeta alrededor del Sol (el tiempo que tarda en dar una vuelta completa alrededor del Sol) elevado al cuadrado es proporcional al cubo del semieje mayor de la elipse. Esto significa que, mientras más grande sea la elipse,
más tardará el planeta en dar una vuelta alrededor del Sol, y el tiempo que le tome está relacionado matemáticamente con el tamaño de la órbita.
En ecuaciones, 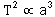 .
.
3
La manzana y la Luna
Isaac Newton nació en Inglaterra a mediados del siglo XVII y estudió en el Trinity College Cambridge, construyendo el primer telescopio reflector (basado en la reflexión de la luz en un espejo, al contrario que los telescopios refractores, que dependían
del paso de la luz por una lente). Newton trabajó mucho en óptica, y se dio cuenta de que la luz no es una entidad única al observar aberraciones cromáticas en su telescopio. De él es el famoso experimento de la luz blanca separándose en sus colores básicos
al atravesar un prisma. Pero ahora nos interesa concentrarnos en su relación con la mecánica de los astros.
Newton creó las leyes básicas de la mecánica:
1- Ley de la inercia: todo cuerpo que no está sometido a ninguna fuerza externa tiene a mantener su estado de movimiento uniforme. Esto significa que un cuerpo en reposo tiende a permanecer en reposo, a menos que se le someta a una fuerza externa. Y un
cuerpo que se mueve, si no está sometido a ninguna fuerza externa, tiende a moverse eternamente siguiendo una línea recta y con rapidez constante.
2- Ley de la dinámica: la fuerza que actúa sobre un cuerpo es igual a su masa multiplicada por la aceleración que sufre, siendo la aceleración la tasa de cambio de la velocidad.
En ecuaciones, F = m . a .
3- Ley de acción y reacción: cuando un cuerpo ejerce una fuerza sobre otro, éste ejerce sobre el primero una fuerza de la misma magnitud y sentido contrario.
Basado en estas (aparentemente) sencillas relaciones, Newton dedujo las leyes de Kepler, suponiendo además que la fuerza gravitatoria generada por el Sol es proporcional a su masa y a la masa del planeta, y que disminuye como el cuadrado de la distancia
entre ellos.
En ecuaciones, 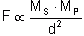 .
.
Ésta es la Ley de Gravitación Universal, y fue una gran avance del pensamiento humano el haber encontrado un paralelismo entre la órbita de un planeta y la caída de una manzana desde el árbol hacia el suelo.
Veamos cómo es esto. Lo primero que debemos recordar es que la primera ley de Newton predice que un objeto que se mueve con velocidad constante, si no sufre el efecto de ninguna fuerza, seguirá moviéndose eternamente con la misma velocidad. Y la segunda
ley de Newton dice que, si el objeto siente la presencia de una fuerza, se acelerará con una aceleración proporcional a esa fuerza. Imaginemos entonces una manzana que cae de un árbol. Sobre ella actúa la fuerza de gravedad, hacia "abajo" (hablando formalmente,
hacia el centro de la Tierra). Al momento de desprenderse de la rama, la manzana está en reposo: su velocidad es cero. Pero de inmediato siente la fuerza hacia abajo, y hacia abajo se acelera. No es difícil imaginar a Newton, como cuenta la leyenda, sentado
bajo el árbol de manzanas. Supongamos ahora que Newton toma la manzana y la lanza horizontalmente. Su velocidad, al ser lanzada, no es cero. La manzana comienza a moverse en dirección horizontal. En dirección horizontal no siente ninguna fuerza, por lo
que tiende a seguir moviéndose con esa velocidad. Pero a la vez, la gravedad tira de ella hacia abajo, por lo que empieza a moverse con velocidad creciente hacia abajo. El resultado es una trayectoria parabólica, hasta que choca contra el suelo. Ahora
bien, ¿qué pasaría si Newton fuera muy, muy fuerte y lanzara la manzana con una velocidad muy, muy grande? Pues que la trayectoria sería más larga. ¿Y si fuera tan larga, que cuando cae hasta la altura del suelo, ya no hay suelo? Imaginemos entonces que
la trayectoria es más larga que el radio de la Tierra. Pues sucederá que la manzana seguirá cayendo eternamente sin tocar jamás el suelo. Justo lo que hace la Luna alrededor de la Tierra. Es éste el principio por el cual se rige el movimiento de los satélites.
En 1687, Newton publicó su gran obra "Philosophiae Naturalis Principia Mathematica", en donde estableció los principios básicos de la mecánica teórica y la dinámica de los fluidos, aplicó el primer tratamiento matemático al movimiento ondulatorio,
dedujo las leyes de Kepler a partir de la ley de cuadrados inversos de la gravitación y explicó las órbitas de los cometas, calculó las masas de la Tierra, el Sol y los planetas con sus satélites, explicó la forma elipsoidal de la Tierra y utilizó esta
idea para explicar la precesión de los equinoccios, además de que estableció la teoría de las mareas. Casi nada. Era una época en que casi todo estaba aún por ser descubierto.
Leonhard Euler fue un matemático suizo del siglo XVIII que hizo algún trabajo en el tema de la astronomía. Sus trabajos mas importantes en astronomía fueron "Theoria Motuum el et de Planetarum Cometarum" (1744), "Theoria Motus Lunaris" (1753) y "Theoria
Motum Lunae" (1772). Usando las leyes de Newton y algunos aportes matemáticos de su propia cosecha, dedujo la órbita de la Luna en términos de tres coordenadas espaciales para definir su posición.
Pero Euler no fue el único que se sirvió de las leyes de Newton para predecir el movimiento de los astros. John Couch Adams, en Inglaterra, y Urbain Leverrier, en Francia, trataron de explicar algunas perturbaciones que habían sido observadas en la órbita
de Urano suponiendo que había un objeto celeste cuya gravedad causara estas perturbaciones. Ellos no trabajaron juntos, cada uno hizo el mismo descubrimiento de manera independiente. Sus resultados predecían la presencia de un planeta, y gracias a ellos,
el astrónomo Galle observó por primera vez a Neptuno en 1846 desde su observatorio en Berlín. Todo parece indicar que la Ley de Gravitación Universal es correcta.
Todavía hoy en día se predice la presencia de objetos estelares usando este enunciado clásico, como podemos ver en los trabajos del astrónomo y astrofísico norteamericano Steven S. Vogt, miembro del Equipo de Búsqueda de Planetas de la Universidad Estatal
de San Francisco. Para muestra, basta un botón:
Seis nuevos planetas con el Medidor Keck de Precisión de Velocidades
Noviembre de 1999
Autores:
Steven S. Vogt (UCO/Observatorio Lick, UCSC)
Geoffrey W. Marcy (Universidad de California, Berkeley)
R. Paul Butler (Departamento de Magnetismo Terrestre, CIW)
Kevin Apps (Universidad de Sussex)
Resumen: Reportamos los resultados de una búsqueda de planetas alrededor de 500 estrellas de la secuencia principal usando el espectrómetro de Keck de alta resolución que tiene una precisión Doppler de 3 m/s durante los últimos 3 años. Reportamos
seis nuevos candidatos fuertes a planetas con órbitas Keplerianas completas, con periodos entre 24 días y 3 años. También proporcionamos parámetros orbitales actualizados para los cuatro planetas anunciados previamente. Cuatro de los seis nuevos planetas
descubiertos tienen masas mínimas menores a dos MJúpiter , mientras que los otros dos tienen masas de aproximadamente cinco MJúpiter . La distribución de masas planetarias continúa mostrando un aumento en las masas más pequeñas. Las excentricidades
orbitales de los nuevos planetas están entre 0,12 y 0,71, lo cual apunta hacia la omnipresencia de las grandes excentricidades. Los 18 planetas extrasolares conocidos que están más allá de 0,2 UA tienen excentricidades mayores a 0,1. El límite de precisión
Doppler actual del medidor Doppler Keck es 3 m/s por observación, como se determinó a partir de observaciones de estrellas estables y residuales con ajustes Keplerianos.
Del resumen anterior podemos ver que en fechas tan recientes como seis años atrás aún se usan las leyes de Kepler en conjunto con el efecto Doppler para encontrar planetas fuera de nuestro Sistema Solar. El efecto Doppler se usa para determinar la velocidad
con la cual se aleja o acerca una fuente de ondas del observador. En nuestro caso particular, la fuente es un astro y el observador es cualquiera de nosotros, usando, claro está, un medidor Doppler. El uso de este efecto se basa en la medición de la longitud
de onda de la fuente, ya que esta longitud de onda aumenta si la fuente se aleja del observador (y lo hace proporcionalmente a su velocidad) y disminuye si la fuente se acerca. Así que, esencialmente, el efecto Doppler nos permite determinar la velocidad
de los objetos celestes.
Con unas pocas leyes de movimiento y una larga serie de efectos derivados de ellas, los hombres encontraron una forma relativamente simple de predecir los movimientos de los objetos celestes, incluyendo algunas de sus consecuencias, como los eclipses.
Las observaciones de la bóveda celeste con telescopios cada vez más poderosos han permitido corroborar que las predicciones son correctas, y las veces en que esto no es así, se ha deducido la presencia de algún objeto celeste no observado previamente.
Esto llevó a descubrir unos cuantos planetas, difíciles de detectar sólo por observación debido a que no emiten luz (sólo la reflejan, y su intensidad es muy baja).
La mecánica celeste está completa. ¿O no? Pronto ésta se vería puesta a prueba, pero esto, señoras y señores, es otra historia.
(Susana Sussmann, © 2005)