







El 9 de julio de 2007 volvió a nevar en Buenos Aires, un fenómeno que no se verificaba desde que el Barón Rojo dominaba los cielos europeos en su triplano Fokker.
Para los que hemos visto nevar muchas veces pero jamás en nuestra ciudad natal, el asunto fue un acontecimiento que mereció festejos, asombro, filmaciones y cantidad de fotos.
¡Nevó en Buenos Aires! ¡Y nevó con temperaturas sobre cero!
Con todo y la extrañeza del suceso, creemos llegado el momento de profundizar algo en este tema.
La pregunta esencial de todo esto es: ¿de dónde salen los copos de nieve? ¿Podemos determinar con precisión su origen y el proceso de su formación? ¿Por qué tienen esas formas tan peculiares, únicas en cada ejemplar y absolutamente singulares dentro de la naturaleza?
La creación de los copos de nieve no es tan distinta de la de las gotas de lluvia. Cualquier meteorólogo nos dirá que las gotitas se forman por la condensación del agua atmosférica alrededor de una microscópica partícula de polvo. Pues bien, cuando la temperatura en las capas altas de la atmósfera es lo suficientemente baja (por una inyección de aire frío o un movimiento ascendente a capas más frías), el agua sufre un proceso de supercongelación que la hace solidificarse. El cristal subsecuente tiene siempre un perfil hexagonal con infinitas y siempre diferentes variaciones individuales.
Esto es simple. Pero, sin embargo, pocos conocen la complejísima física que se esconde tras el génesis de estas maravillosas gemas con que el cielo nos regala de cuando en cuando.
Pero nosotros no nos conformamos con el "pocos conocen". Queremos ser parte de ese selecto grupo. Y para ello necesitamos a Kenneth Libbrecht.
El doctor Kenneth Libbrecht es profesor de física en el CalTech, y uno de los que mejor han estudiado el proceso de formación de los cristales de hielo en los copos de nieve. "Cualquiera pensaría que la física de los copos de nieve se conoce perfectamente", explica Kenneth. "Pero, muy por el contrario, una mirada de más cerca nos revela que hay algunas preguntas muy básicas al respecto que permanecen sin respuesta".
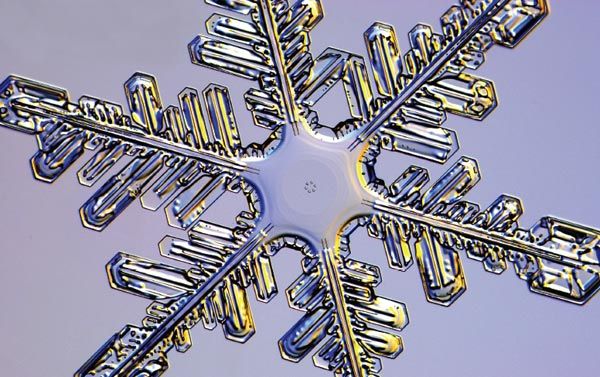
Aunque hoy en día podemos predecir con total exactitud la posición de casi cada átomo dentro de moléculas de cualquier grado de complejidad (pongamos por caso enormes macromoléculas proteicas), en el copo de nieve hay un difícil problema de dinámica molecular que nos impide predecir exactamente la forma que tendrá.
Sí podemos asegurar que el perfil general de todos los copos siempre será hexagonal. Y lo será debido a la forma de la molécula de agua: ésta es triangular, un perfecto triángulo equilátero (con los tres lados iguales). A partir de ella, cada nodo de crecimiento del cristal se formará en un ángulo de exactamente 60 grados con respecto a los vértices del triángulo. Con la continuidad de este proceso, seis de estos triángulos moleculares formarán el marco del crecimiento ulterior, y esta forma será siempre hexagonal.
Esta es la parte estática del proceso; el aspecto dinámico —si formará facetas o no, si será único o se fragmentará en subunidades más pequeñas— depende de la ubicación espacial de cada uno de los átomos que se agregan a la estructura, y este problema de crecimiento es lo suficientemente complicado como para ser impredecible, incluso en cristales de agua relativamente simples como el hielo. La increíble variedad de formas de los copos de nieve demuestra nuestra ignorancia al respecto. Por ejemplo, si uno examina dos nevadas distintas, separadas por sólo algunas horas, puede encontrar en una de ellas cristales cuyas agujas son 50 veces más largas que anchas, mientras que en la otra las diferencias serán de solo 20 veces. ¿Cómo puede ser que se produzcan estructuras tan diferentes a partir de exactamente el mismo material?
Libbrecht tiene una buena explicación: "Cada columna, aguja y placa de forma estrellada que nos cae del cielo, comienza como un sencillo prisma hexagonal, que es la forma básica de un cristal de nieve. Esta forma básica tiene dos facetas que llamamos `basales´ y seis facetas `prismáticas´. Sin embargo, la estructura final depende de las velocidades de crecimiento relativo en las superficie de las facetas: el vapor se condensa más rápidamente en las caras prismáticas. El mero hecho de que existan cristales columnares y planos exige que la velocidad de crecimiento varíe en un factor de 1000 bajo diferentes condiciones".
Aún aceptando esta realidad, es difícil imaginar una explicación para la infinita variedad de formas que puede rendir este único proceso, la condensación y supercongelación del agua sobre una misma estructura básica. Entonces, la solución no pasa ya por observar y estudiar los cristales finales, sino en tratar de comprender el proceso de su crecimiento individual, ya que allí residen las diferencias.
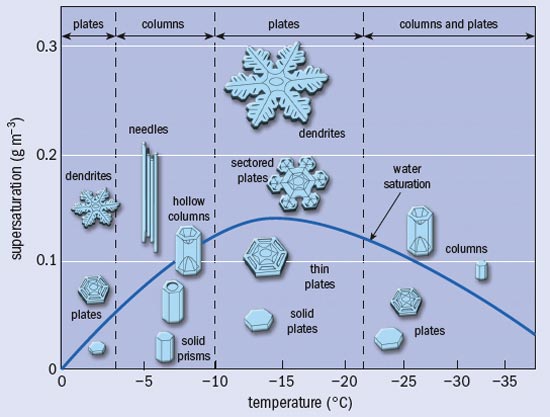
Preocupado por este mismo asunto, el físico de la Universidad de Hokkaido Ukichiro Nakaya comenzó, alrededor de 1930, a "cultivar" y hacer crecer sus propios copos de nieve en su laboratorio., única forma de estudiar su proceso de formación bajo condiciones controladas. Sus observaciones se resumen hoy en un diagrama morfológico de los cristales, que considera sus formas como funciones de la temperatura y la humedad. En éste, la temperatura ocupa el eje x y la humedad el y. El eje vertical se representa por encima del 100% de humedad, y por eso se lo llama "sobresaturación" (de agua). La línea azul (la "línea de saturación") muestra las diferencias de diseño entre los cristales formados por encima y por debajo de ella.
Observando el diagrama de Nakaya hay dos circunstancias que inmediatamente saltan a la vista. Una es que los cristales relativamente simples comienzan a volverse más y más complejos a medida que aumenta la humedad; las formas estrelladas y con múltiples ramas sólo se forman en altísimas condiciones hídricas.
Segundo, se verifica que la forma general se comporta peculiar y dramáticamente como función de la temperatura, cambiando de formas de placa a formas columnares cuando la misma desciende, y revirtiendo lentamente a placas si la temperatura sigue bajando. Esta última circunstancia ha demostrado ser particularmente difícil de explicar, y, en efecto, 75 años después de los estudios del sabio nipón aún seguimos sin entender el porqué de esos grandes cambios morfológicos causados por apenas unos pocos grados de diferencia.
En 1975, otro japonés, Takehiko Gonda, de la Universidad de Tokio, demostró que los cristales que habían crecido en un ambiente de baja presión eran más simples que aquellos formados a alta presión atmosférica. Es decir que no sólo intervenían dos variables, sino al menos tres. Y puede haber más: "De hecho, el diagrama morfológico de los cristales de nieve es una simple `rebanada´ bidimensional de una realidad mucho más compleja y multidimensional. Si agregamos un tercer eje —el tiempo—, veremos que los cristales se hacen mucho mayores y más complejos conforme pasa el tiempo, u otro eje que muestre que lo mismo ocurre al aumentar la presión", explica Libbrecht.
Como el conocimiento acabado del proceso necesariamente tiene que contemplar todas las variables, y a nosotros nos faltan algunas, o tal vez muchas, todo el asunto debe considerarse investigación aún en proceso. No gobernamos ni siquiera todos los factores intervinientes en el laboratorio, así que no podemos ni empezar a hablar de lo que debe ocurrir en la atmósfera alta. A medida que el cristal va cayendo hacia tierra, atraviesa muchísimas capas de aire, cada una de ellas con condiciones de temperatura, viento, humedad, velocidad, presión y dirección completamente diferentes. Y es la trayectoria individual de cada copo la que determina su forma final, por lo que son los zarandeos y remolinos que lo conducen la razón de que no haya dos iguales. Pero los seis brazos sí que son idénticos... esto se debe a que los seis viajan juntos y por lo tanto han compartido las mismas condiciones a través de todo el trayecto.
Las condiciones atmosféricas, a su vez, definen el modo en que cada molécula de agua es transportada hasta el copo en sí. A medida que el cristal absorbe las moléculas del entorno, su espacio circundante se va viendo cada vez más despoblado. Entonces, la difusión debe encargarse de traerle el agua desde distancias cada vez mayores. He aquí la causa de que las puntas del copo tiendan a crecer más que el centro: la punta gira a mayor distancia que la parte central, alcanzando regiones que lógicamente contienen más vapor de agua. Esta retroalimentación positiva (los brazos crecen más rápido porque alcanzan regiones más lejanas, y cada vez alcanzan regiones más lejanas porque son capaces de crecer más rápido) genera espontáneamente estructuras cada vez más complejas (que se retroalimentan porque son más complejas, y son más complejas porque se realimentan). Es de este modo que se forman las ramas dendríticas y también las de forma estrellada.
En realidad, todo el proceso depende de las ecuaciones diferenciales; de una de ellas, concretamente la llamada Ecuación de Difusión. Esto se sabía (ya hemos explicado por qué la difusión del vapor de agua es absolutamente crítica en la formación de los cristales). Pues bien, fue recién en 1947 que el matemático soviético G. P. Ivantsov descubrió una serie completa de soluciones para la Ecuación de Difusión, que se mantenían completamente estables en todas las condiciones de humedad, temperatura y demás variables implicadas en el crecimiento de los cristales, explicando, además, cómo cambia la densidad del material mientras se produce la difusión. Actualmente se conocen como Ecuaciones de Crecimiento de Ivantsov, y son una herramienta clave para comprender la creación de las complejas estructuras de los copos.

Representadas tridimensionalmente como paraboloides en forma de aguja o como parábolas en dos dimensiones, ellas muestran agujas que se alargan a medida que la difusión deposita partículas de agua sobre la superficie de los cristales, preservando la forma de las agujas a lo largo de todo el proceso de crecimiento. O sea que tanto el radio de curvatura de la prominencia como su velocidad de crecimiento permanecen constantes a lo largo de todo el proceso. Lo interesante es que estos descubrimientos experimentales del día de hoy fueron predichos hace 60 años por las Soluciones Ivantsov, que adicionalmente tienen la particularidad de ser tan generales como para permitir cualquier radio de curvatura en las puntas, demostrando además que el ritmo de crecimiento de cada una es inversamente proporcional al radio.
Pero existen enrrevesados problemas de física asociados con las ecuaciones de difusión que debemos resolver antes de dar con la solución correcta entre las múltiples que Ivantsov nos ofrece como posibles. Estos problemas dependen nada menos que de la dinámica de la agregación molecular durante la formación del cristal. Es decir que un efecto macroscópico fácilmente observable (el crecimiento apical de los cristales) depende de complejísimas interacciones a nivel molecular.
Los cristales crecen casi exactamente igual, con independencia del tipo de agua que utilicen como materia prima: el cristal resultante será el mismo si se parte de vapor de agua supercongelado o de agua líquida en suspensión. En este caso la difusión del calor generado en la interfase limita el crecimiento, mientras que el crecimiento de un cristal de vapor está limitado por la difusión de las moléculas de vapor de agua. Entonces, si los procesos son distintos, ¿por qué el cristal generado es el mismo? Porque ambos son descriptos por la misma Solución de Ivantsov.
Como estas ecuaciones son críticas para la estructura y la apariencia del cristal final, y son afectadas por múltiples factores, suelen producirse situaciones extraordinarias.
Los campos eléctricos de alta intensidad inducen fácilmente el crecimiento de cristales en el extremo desnudo de un cable. Esto se debe a que hay una mínima carga eléctrica en el aire que circunda al hilo, por lo que la superficie del hielo se carga a su vez. Esta circunstancia produce hermosos cristales, más o menos dúctiles, más o menos densos, dependiendo de las tensiones que se apliquen al cable.
Estas características están siendo estudiadas hoy en día por la industria metalúrgica, que ya está comenzando a imitar a la naturaleza para gobernar ciertos atributos de sus metales, congelándolos mientras se encuentran fundidos y aplicándoles fuertes campos eléctricos.
En definitiva, las bellas, complejas y maravillosas formas de agua sólida con que la naturaleza nos regala en ocasiones, tienen vericuetos que ni siquiera hoy llegamos a comprender. Sin embargo, las sutiles leyes que las controlan recién comienzan a desentrañarse. La dificultad de este aprendizaje no obsta para que nos extasiemos cada que vez que se nos presenta la oportunidad, en la contemplación de estas hermosas joyas que pueblan los aires.



