Juan Pérez salió de su casa arrastrado por Cacique, que babeaba y tironeaba de la correa como si su vida dependiese de ello. Corrieron juntos hacia el árbol más cercano. Juan tiró de la correa, intentando guiar al ansioso cuadrúpedo hacia el árbol de la vecina. Tras un corto forcejeo el joven logró su objetivo, consiguiendo como premio unos segundos de respiro.

Mientras Juan se reponía, Cacique controló que todo en el árbol estuviese en orden y procedió a dejar su impronta líquida en el tronco; ya buscaría un mejor lugar para sus deposiciones sólidas.

Juan vio asombrado el fluido que alegremente emanaba de su fiel mascota. Era un fino chorrito, pero formado esta vez por puntos del tamaño de granos de arena. Pequeños y numerosos puntos amarillos y negros.

Cacique levantó la cabeza. "¿No podrías mirar para otro lado?" pareció decir con sus grandes y brillantes ojos cuadrados. Juan se quedó congelado. Quizás había tenido demasiado trabajo en la semana.

Aprovechando que su amo parecía más tonto que de costumbre, el animal se lanzó a toda velocidad en dirección a la plaza. Juan, aferrado a la correa, flameó tras él.

Cuando llegaron, el joven liberó al Canis lupus, subespecie desconocida, y se sentó en un banco mientras Cacique correteaba unas palomas que, ofendidas por semejante desvergüenza, se retiraron con magnificencia hacia parajes más tranquilos.

Juan empeoraba, ahora todo lo veía cuadriculado. Las palomas alzando vuelo, los autos, las nubes. Los árboles eran una densa filigrana de luces y sombras cuadriculadas. Los paseantes le devolvían la mirada con cuadriculada desconfianza. Los niños jugaban en el arenero, que no era otra cosa que una gigantesca trama cuadriculada con millones y millones de celdas negras y blancas. Los alborotadores infantes interactuaban entre sí, pseudoaleatoriamente, en estructuras y formas efímeras que cambiaban con rapidez de configuración. Juan recordó las famosas películas de los hermanos Wachowski y luego la mucho más antigua novela, Ubik, de Philip K. Dick. ¿Se repondría? ¿Debería buscar un psicólogo?

Nunca debió haber leído ese pequeño e inocente artículo en Axxón.

Considérate avisado, gentil lector, nunca más volverás a ver la vida con los mismos ojos: Hablaremos de los autómatas celulares.

Arthur Clarke escribió "Cualquier tecnología lo suficientemente avanzada es indistinguible de la magia". Tal es la sensación del profano cuando se introduce en el tema y se percata de que esta nueva magia toca casi cualquier rama de la ciencia: Crecimiento y propagación de células cancerosas. Epidemiología. Finanzas y Economía. Crecimiento de cristales. Patrones de pigmentación en caracoles. Topobiología y biología del desarrollo. Dispersión de árboles dentro de un ecosistema. Teoría de la relatividad. Reacciones químicas. Dinámica de poblaciones. Coevolución. Geología. Puntos cuánticos. Tráfico vehicular. Evacuación de barcos en emergencia. Redes neuronales e inteligencia artificial. Criptografía. Termodinámica e hidrodinámica y un muy largo etcétera, etcétera, etcétera.

Con respecto a la hidrodinámica, no hemos encontrado aún trabajos sobre excreciones líquidas en C. lupus, pero no sería de extrañar que en cualquier momento alguien dé a conocer un sesudo informe sobre el tema empleando esta revolucionaria herramienta.

Las aplicaciones científicas no acaban ahí ni mucho menos y las artísticas son tanto o más variadas que las científicas. Desde "efectos" implementados en los más conocidos programas comerciales de diseño gráfico (blur, emboss, detección de bordes y emulación de estilos como Seurat, Sezanne, Monet, etc). Hasta gráficos tipo "plasma", que recuerdan vaporosas nubes, música sintética y efectos especiales utilizados en películas como Final Fantasy, Matrix y El Señor de los Anillos I, II y III."

Pero, antes que nada, ¿qué es un autómata celular? En pocas palabras, un autómata celular (AC) es una matriz, donde las celdas cambian o no de estado, tomando por ejemplo valores de cero o uno, a cada golpe de reloj. El nuevo valor obedece a leyes simples que evalúan los estados de las células vecinas. Si se logran las configuraciones y las leyes adecuadas, pueden obtenerse objetos rebosantes de complejidad y belleza, como el fondo de esta página.

Stanislaw Ulam

Los autómatas celulares fueron inventados a fines de los cuarenta por Stanislaw Ulam (1909-1984) y John von Neumann (1903-1957).

Ulam fue principalmente matemático, inventó el método de simulación Monte Carlo y aportó importantes contribuciones a la teoría de los números y al análisis matemático. Junto con Eduard Teller inventó la bomba de hidrógeno.

Von Neumann trabajó en los más variados campos. Colaboró en los fundamentos de la teoría de la mecánica cuántica, incursionó en economía y en la teoría de los juegos. Junto con Herman Goldstine diseñó la arquitectura lógica de la primer computadora electrónica.

Tal es el tamaño de los padres de la criatura.

Jonh von Neumann

En 1948, Von Neumann presentó a la comunidad científica un trabajo donde se preguntaba si una máquina podía realizar copias de si misma partir de elementos simples o si había algo mágicamente extramecánico en la autoreproducción (Feymann inició el debate en los sesenta y Drexler retomó la idea en los ochenta originando la fiebre de la nanotecnología). Von Neumann luego demostró matemáticamente que sí era posible la existencia de tales robots. Junto a Ulam, en Los Álamos, desarrolló los primeros autómatas celulares para modelar el concepto. Ulam sugirió que en vez de piezas elementales se consideraran diferentes estados numéricos representando las distintas partes de la máquina autorreplicante. Los autómatas celulares estaban naciendo.

Existen muchas variaciones de AC. Los más simples se desarrollan en una dimensión. Imaginen una fila de células, cada una evaluando constantemente a sus dos vecinas para decidir de qué color teñirse. Presentadas todas las generaciones en un mismo plano, el modelo puede evocar con eficacia ciertos patrones de pigmentación en caracoles.

Caracol marino con pigmentación similar a un autómata celular

Autómata celular con patrones similares a los de un caracol marino

Autómatas celulares lineales. Los gráficos de la izquierda muestran el crecimiento, de arriba hacia abajo, originado a partir de una línea de datos aleatoria y para cuatro grupos de leyes distintas. Los gráficos de la derecha examinan las mismas leyes partiendo de una línea con un solo "1" central

Dando valores aleatorios a la primer generación se obtienen diversos patrones, aunque puede discernirse el estilo básico de cada grupo de leyes. Cuando estas últimas cambian, los patrones obtenidos son radicalmente diferentes. Aunque se presenten en dos dimensiones, debe recordarse que sólo existe una generación o línea a la vez.

La misma idea puede trasladarse al universo bidimensional. En los autómatas celulares de trama cuadriculada, cada célula se puede considerar como viviendo en un vecindario de cinco o nueve células, ella misma incluida. Esto según sean los vecinos que toman parte de la reunión de consorcio en la que se decide si el vecino del centro es echado o no de su departamento. Hay infinitas variaciones de estos vecindarios, que han ido creciendo en tamaño conforme al aumento de potencia computacional disponible.

Vecindarios de celdas adyacentes examinadas por las leyes. Vecindario Von Neumann para cinco vecinos (a) y vecindario Moore para nueve (b)

Las siguientes imágenes se obtuvieron de un modelo de reacción y difusión de reactivos y productos químicos basado en un AC de dos dimensiones.

Tramas de Chita y Leopardo generadas por simulación tipo cascada de reaccion-difusión química. La fila inferior se generó a partir de la superior. Turk 1991

Trama de jirafa. El gráfico de la derecha se graficó procesando el de la izquierda con un generador de líneas. Turk 1991

También se han desarrollado AC donde las celdas son triangulares o hexagonales. Estos planos pueden considerarse como casos particulares del plano cuadriculado.

Hagamos un alto para dedicarles unas palabras a los fractales, más precisamente al Triángulo de Sierpinski. Partiendo de un triángulo equilátero, réstesele un triángulo igual de forma que queden tres triángulos idénticos. Repita infinitamente la operación con los triángulos obtenidos y tendrá en sus manos un hermoso y saludable triángulo de Sierpinski.

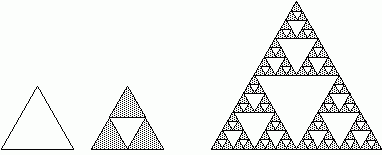
Triángulo de Sierpinski en construcción. El primer triángulo representa el axioma, el segundo el generador, es decir la resta del triángulo central, y el tercero es el triángulo de Sierpinski luego de cuatro iteraciones

Hay muchas formas de obtener el objeto en cuestión. Algunas de ellas utilizan autómatas celulares.

Pirámide Sierpinski realizada por el autor de este informe a partir de sucesivas generaciones de un AC bidimensional. Sólo las caras exteriores presentan triángulos de Sierpinski, el resto de la pirámide puede considerarse como una acumulación de derivados del mismo triángulo luego de pasar por la maquinaria del AC. Una de las células del autómata celular mutó a una forma agresiva y se comió el tilde de la palabra "Axxón", sepan disculpar la naturaleza impredecible de los AC

En el universo bidimensional puede encontrarse un mundo de lo más extraño, el mundo alambre. En este mundo, descubierto por Brian Silverman en 1987, las celdas pueden tener cuatro valores: Fondo, alambre, cabeza de electrón y cola de electrón.

Las celdas con valor "fondo" no cambian. Las del tipo "alambre" se transforman en "cabeza de electrón" si tienen una o dos vecinas "cabeza de electrón". Las "cabezas de electrón" se transforman siempre en "cola de electrón" y éstas decaerán en "alambre" invariablemente.

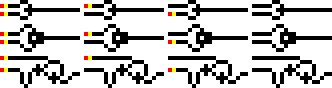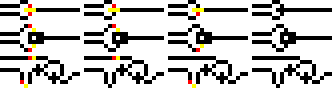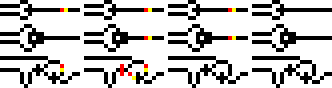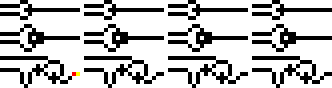
Puertas lógicas en mundo alambre. OR, XOR y AND en orden descendente. Las columnas ejemplifican las cuatro combinaciones de entradas: 11, 10, 01 y 00. OR entrega un valor 1 si recibe un 1 en una o ambas entradas. XOR hace lo mismo pero sólo si una sola entrada es 1. AND da como resultado 1 sólo si ambas entradas son 1

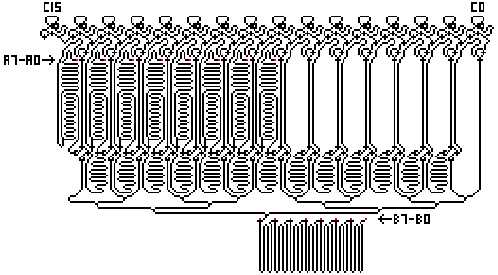
Multiplicador de dos numeros binarios de ocho bits. Nick Gardner 2002

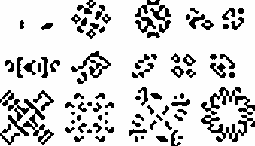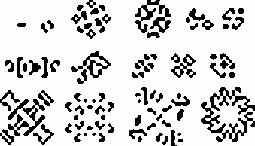
Quince osciladores de período 2

"Si tienes tres vecinos vivos, naces. Con dos o tres vecinos vivos, tu estado no cambia. De cualquier otra forma mueres". Estas son las reglas que rigen la vida y la muerte en el universo de los AC, en la popular versión, creada por John Horton Conway, de la Universidad de Cambridge, llamada "Game of life", "Life" o "Juego de la Vida". La simplicidad de las reglas puede engañar al lector desprevenido. La complejidad y el caos acechan por doquier entre los AC. Examinemos algunos objetos del universo explorado por el programa de Conway, del que, en 1974, una nota en Time dijo: "Millones de dólares en valioso tiempo de cómputo han sido desperdiciados por la creciente horda de fanáticos del juego". En el presente la cifra puede haber crecido al orden de los cientos de millones de dólares y la palabra "desperdiciados" es más que cuestionable.

Algunos especímenes son estáticos. Su configuración es tal que no muere ninguna de sus celdas ni nacen células adyacentes. Pueden parecer aburridos, pero es un mérito mantenerse inmóvil en un mundo tan reactivo. Estos objetos son utilizados luego con profusividad en la construcción de estructuras más complejas.

Tres osciladores de períodos 5, 10 y 30. En el centro, oscilador de período 30, formado por cuatro osciladores que funcionan como rebotadores de gliders (explicados más abajo), girándolos 90° para cerrar el circuito. Arriba a la derecha, un oscilador tipo cerca eléctrica de período 5. Esto tipo de osciladores son de longitud infinita, pueden construírse de cualquier extensión. Abajo a la izquierda, un oscilador de período 10. La estructura circular bajo este es un estático llamado "panal", no modifica ninguna de sus celdas. Su aparente movimiento se debe a un error del programa gráfico utilizado para aumentar el tamaño de la imagen o, más probablemente, al miedo de las celdas por la cercanía de la hambrienta celda mutante. La velocidad de la animación ha sido ralentizada para permitir observar las formas con claridad

El más simple objeto estable que puede encontrarse es un oscilador de tres puntos en línea. Un oscilador muta en varias formas para volver, luego de n clicks de reloj, a la primer forma de la secuencia. Como la primer y última forma son iguales, el oscilador entra en un bucle infinito, repitiendo constantemente los mismos patrones. Existen muchos osciladores, llegando algunos a evolucionar durante más de 30000 clicks de reloj antes de volver al primer estadío.

Un tipo especial de oscilador son los gliders ya mencionados. La última configuración y la primera sólo difieren en una cosa, la posición, produciéndose así el movimiento del objeto.

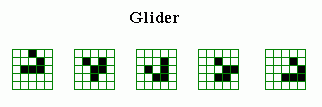
Las cuatro formas del más pequeño glider. La quinta figura es idéntica a la primera, sólo que desplazada una celda en diagonal

Naves avanzando hacia la derecha

A los gliders más grandes se les llama naves espaciales. Hay naves bastante grandes, algunas son llamadas puf-puf porque dejan una estela de basura o humo a su paso. Un cañón es una estructura que fabrica gliders constantemente. Algunos puf-puf dejan una nube aparentemente aleatoria, que luego de algunos ciclos se transforma en un cañón.

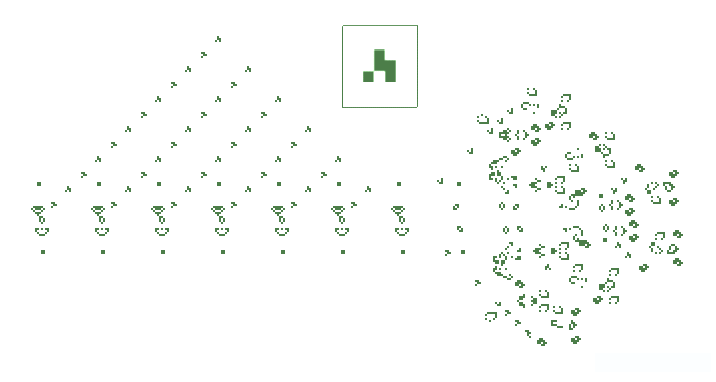
Puf-puf que siembra a su paso cañones que llenan el espacio de gliders

Una estructura mayor aún es la base espacial.

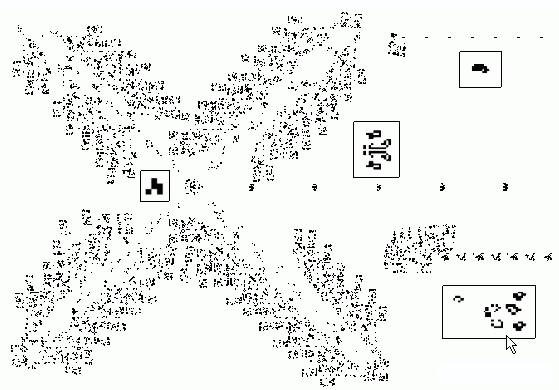
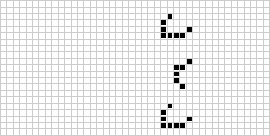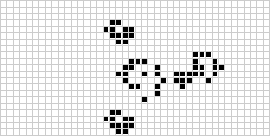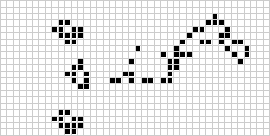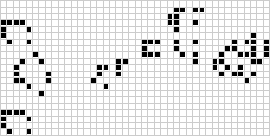
Base espacial y dos cañones)]. Cuatro chorros de 63 gliders en total colisionan para formar la nave espacial en el centro de la base. Cada 416 clicks de reloj se construye una nave que avanza a velocidad 2/5, es decir dos celdas cada cinco clics de reloj. La velocidad máxima de cualquier objeto es, evidentemente, 1. La base es obra de Dave Green y la nave de Noam Elkies. Dieter Leithner construyó los dos cañones. El superior fabrica un glider de velocidad 2/4. El inferior produce un puf-puf ecológico de igual velocidad. Nótese el "silenciador", señalado por la flecha, que elimina el humo. Sin este agregado la nave sería un puf-puf sucio, formado por los tres elementos de la derecha, y la suciedad formada, arriba del silenciador, terminaría destruyendo la base espacial y los dos cañones

Pufpuf sucio avanzando hacia la izquierda

Hay naves que fabrican naves, son llamadas naves madre o nodrizas. Se han fabricado contadores en base cuatro que además disparan un glider cada 30.000 clics.

Cañón contador base cuatro disparando un glider, señalado por el cursor, luego de 30000 clicks, acompañado de un cañón de frecuencia 30)]. También se han desarrollado contadores decimales, que producen una columna de números del cero al nueve

Contador digital de Alan Hensel. Los números avanzan hacia arriba. Luego del 9 vuelve a repetirse la secuencia

Hemos encontrado en la web un buscador de números primos, una fábrica de naves madre que fabrican a su vez gliders, una máquina sumadora en base binaria, cañones pseudo aleatorios de período de 152.880 y un monstruoso oscilador de período 97.307.852.687. Una de las más extrañas construcciones encontradas fue una celda del juego de la vida. Así es, una compleja trama de 500x500 celdas que emula la maquinaria del juego de la vida. Interactúa con las "celdas" vecinas cambiando su estado según los estados de las macroceldas adyacentes, en un lento pero asombroso metajuego de la vida.

Cabe destacar que en las primeras épocas del juego de la vida, los objetos eran encontrados a mano por los exploradores. Cualquier nube aleatoria desprende siempre algún que otro glider y deja tras la explosión inicial una miríada de objetos estáticos y osciladores simples donde experimentar en busca de nuevas formas. En la actualidad existen programas que examinan muchísimas configuraciones buscando osciladores de períodos largos, naves espaciales originales y otros raros especímenes. Aún no se ha encontrado un objeto que se copie a sí mismo pero su búsqueda continúa. Observe, amable lector, que "La naturaleza de los autómatas celulares impide su estudio por la aproximación matemática clásica", según palabras de Stephen Wolfram, el prócer más encumbrado y por mucho de esta nueva ciencia. Se requiere de programas de búsqueda para encontrar algunas estructuras que escapan a la imaginación. Aunque se utilice la computadora como herramienta de trabajo, los diseños más complejos necesitan también del hombre para asistir en su desarrollo. Invitamos al amable lector a zambullirse en las aguas del universo de Conway, quizás pesquen algo interesante.

En el universo 3d, las cosas adquieren otra dimensión. Pueden verse equivalentes de gliders, osciladores, estáticos, naves espaciales y demás pululando por las aguas matriciales.

Autómata celular 3D

Pero volvamos a la realidad. En 1996, Nicholas J. Savill y Paulien Hogeweg de la Universidad de Utrecht, Holanda, presentaron un modelo que describe la morfogénesis en sistemas celulares simples. Cuando el alimento escasea, las amebas se agregan en forma de tren o babosa, para reptar en busca de una zona donde alimentarse. El paso de organismo unicelular a multicelular es regulado por la producción y quimotaxis al AMPc, molécula usada como señal de agregación y de adhesión celular. El modelo de AC emuló con exactitud los diferentes estadíos en el proceso de morfogénesis.

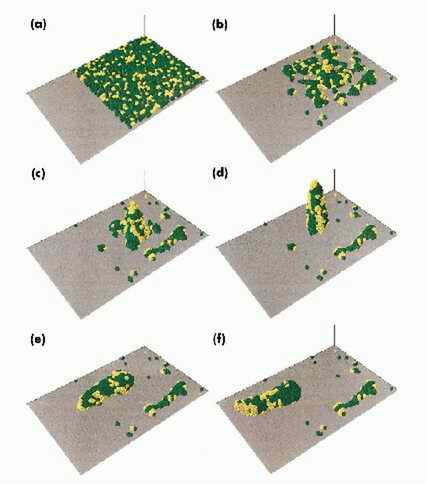
Secuencia de la simulación de agregación de Dictyostelium. a) Distribución aleatoria de amebas. Los colores verde y amarillo indican diferentes estados de maduración. b-c-d) Migración de las amebas unicelulares hacia la forma de columna multicelular, coordinada por AMPc. e) Caída de la columna. f) Comienzo de migración de la forma de babosa. La velocidad de migración del agregado multicelular es mayor que la de la ameba unicelular

Tim Meyer-König, Hubert Klüpfel y Michael Schreckenberg estudiaron la evacuación de naves en situación de emergencia. Comprobaron con sus investigaciones que es posible simular escenarios y comportamientos complejos con un modelo elemental. Se puede evaluar así el tiempo de evacuación de un barco con exactitud y precisión. Una compañía, TraffGo, otorga consultorías y certificados de prestigio internacional con la asistencia de un programa similar para evaluar la evacuación de barcos y diversas estructuras.

Comparación de realidad y simulación en un ejercico de evacuación

Sarit Moldovan y Jacob Goldenberg, de la Universidad Hebrea de Jerusalén, investigaron la resistencia social a las innovaciones, desde el punto de vista del marketing. Realizaron modelos de poblaciones de consumidores teniendo en cuenta la publicidad "de boca en boca", es decir los consejos que gente conocida se ofrecen y demandan entre sí. La publicidad de boca en boca puede ser tanto positiva como negativa. Se plantearon tres tipos de consumidores: Lideres de opinión, que militan a favor de la adopción del nuevo producto, líderes de resistencia, que abogan por su no adquisición y consumidores normales, la gran mayoría de la población. Los consumidores normales también ejercen la publicidad de boca en boca, pero su esfera de contactos es menor y su opinión incide con menor fuerza entre sus conocidos. La publicidad externa, es decir la acción de la campaña publicitaria, puede no ser la fuerza que más impacte en un mercado dado. Incluso puede generar líderes de resistencia. Este comportamiento complejo es ideal para ser modelado por AC, donde las células interactúan a distancia y no sólo en su entorno inmediato. Incluso en los casos de productos exitosos, el "boca en boca" negativo puede ser una fuerza invisible que dañe la imagen del producto causando perjuicios irreparables en el mercado. Es entonces cuando sobrevienen los derrumbes estrepitosos. En estas situaciones incrementar los esfuerzos de publicidad no tiene sino una pequeña incidencia en la dinámica del mercado. Esto puede explicar por qué Jeffrey P. Bezos, fundador y jefe ejecutivo de Amazon.com, encontró que la publicidad simplemente no justificaba su costo. Como resultado Amazon.com (Marzo del 2003) limitó cualquier tipo de publicidad y confió sus esperanzas en la publicidad "de boca en boca". En este trabajo y en muchos otros similares se observa la eficacia de los AC a la hora de analizar procesos sociales complejos.

Tom Ostoma and Mike Trushyk, del "Los Alamos National Laboratory", mismo laboratorio donde trabajaron Ulam y von Neumann, propusieron una inquietante teoría que sacude los pilares de la física moderna. El universo no es otra cosa que, oh sorpresa, un gigantesco autómata celular. Según esta teoría, vivimos en una increíblemente densa trama tridimensional donde el largo de una celda es también la mínima distancia posible, la distancia de Plank, 1,6 x 10^-35 metros. El tiempo también está cuantizado, siendo el mínimo intervalo 5,4 x 10^-44 segundos, la constante temporal de Plank.

Desgraciadamente el hardware del autómata celular universal no es medible mediante métodos directos. Por definición, se encuentra fuera de nuestro universo y será inaccesible por siempre ya que estamos formados por las mismas celdas que él apaga y enciende. Las leyes físicas que lo gobiernan no tienen por qué ser iguales a las nuestras. De hecho, todas las celdas del universo se actualizan a la vez a cada golpe de reloj. Tamaña potencia de cálculo escapa a nuestra imaginación a mayor velocidad que la luz. Los autores proclaman además que la Teoría de la Relatividad Especial es congruente con un universo autómata celular. Proponen esta idea en un extenso análisis que también escapa a gran velocidad del objetivo de este informe. Ellos concluyen: "...Así, hemos descubierto que la relatividad especial se deduce directamente del modelo autómata celular del universo, una vasta computadora autómata celular tridimensional. En el proceso, hemos descubierto la verdadera naturaleza del movimiento de la luz y del principio de la relatividad. En el proceso, hemos revelado el proceso cuántico oculto tras la inercia newtoniana clásica" .

El hecho de si esta humilde y poco ambiciosa teoría es absolutamente correcta, si aporta algunos elementos innovadores o si es errónea de pies a cabeza aún es materia de discusión. Lo que está fuera de dudas es que su sola existencia nos revela mucho sobre la potencia que tienen los autómatas celulares.

Medita sobre todo esto cada vez que camines sobre baldosas.

BIBLIOGRAFÍA Y MÁS DATOS:

Artículos de Stephen Wolfram, el gurú de los AC
A New Kind of Science" de Stephen Wolfram. Libro que recoge diez años de trabajos con AC
Excelente programa freeware de autómatas celulares. Utiliza DirectX. Puede además barse archivos con miles de objetos. Absolutamente recomendable. Luego de su uso se aconseja visitar a un especialista en adicciones.
Programa Capow, de Rudy Rucker. Generador de autómatas celulares de gran colorido y diversidad
Diversas contribuciones a los autómatas celulares
Simulación de evacuación en barcos de pasajeros
Resistencia a las innovaciones modelada por AC
Teoría de la relatividad especial, velocidad de la luz y autómatas celulares

(Diego Escarlón, © 2005)