Vivimos días excitantes. Los físicos del siglo 21, armados de instrumental
que no soñaban disponer hace apenas diez años, se encuentran constantemente
ante nuevas y revolucionarias fronteras y deben aceptar cambios abruptos de concepto.
La edad del Universo. Materia y energía oscura. El universo plano. Materia que se enfría
al aplicarle energía. Fantasmales globos de fuego en el espacio ingrávido. Medición de
un momento anómalo en un muón que atenta contra el modelo estándar de partículas...
Aunque suenen raros, varios de estos temas se están discutiendo hoy en la comunidad científica y aparecerán
en el Zapping. No se trata de seudociencia o de interpretaciones esotéricas:
la Física de verdad se está remodelando. Encaramos aquí las implicaciones de una serie
de experimentos cuyos resultados ayudarán a definir cuestiones tan importantes como la
unificación de las fuerzas y la existencia de más dimensiones:
La fuerza de atracción entre dos superficies en el vacío —que
predijo Hendrik Casimir hace más de 50 años— puede afectar todo,
desde las micromáquinas a la Teoría Unificada.

HENDRIK CASIMIR
|
|
¿Qué ocurre si uno toma dos espejos y los coloca en un recipiente donde se ha
realizado el vacío de tal modo que queden cara a cara y muy próximos? La primera
respuesta que a uno se le ocurre es "nada de nada". En realidad los espejos
se atraerán entre sí, justamente a causa de la presencia del vacío y de los
efectos cuánticos que se producen en él.
Este sorprendente fenómeno lo predijo en 1948 el físico teórico alemán Hendrik Casimir
cuando trabajaba con soluciones coloidales en los Laboratorios de
Investigación de Philips en Eindhoven, Alemania. El fenómeno se llama ahora Efecto Casimir
y la fuerza de atracción que se produce entre los espejos es conocida como la Fuerza de
Casimir.
El Efecto Casimir fue, por muchos años, apenas una curiosidad teórica. Pero en los
últimos años se ha disparado un creciente interés en este fenómeno. Los físicos
experimentales han notado que la Fuerza de Casimir afecta el funcionamiento de
las partes de las micromáquinas que se intentan construir hoy, al mismo tiempo
que los avances producidos en los instrumentos de medición permiten medir esta
fuerza con una precisión imposible de lograr en el pasado.
Los físicos fundamentales también impulsan este redescubrimiento. Muchos teóricos
han predicho la existencia de "grandes" dimensiones en la "Teoría de campo unificado
de las fuerzas elementales de diez y once dimensiones". Esas dimensiones, dicen ellos,
pueden modificar la gravitación newtoniana clásica a distancia de menos de un
milímetro. La medición del Efecto Casimir puede ayudar a los físicos, entonces,
a probar la validez de esas ideas radicales.
¿Qué es la Fuerza de Casimir?
Aunque la Fuerza de Casimir parece chocar por completo con toda intuición, en realidad
se la comprende muy bien. En los viejos días de la mecánica clásica, la idea de
vacío era simple: el vacío es lo que queda si uno quita hasta la última partícula
de un recipiente y reduce la temperatura al cero absoluto. Con el arribo de la mecánica
cuántica, sin embargo, nuestra noción del vacío ha cambiado por completo. Todos
los campos —particularmente los campos electromagnéticos— tienen
fluctuaciones. En otras palabras, a cada momento el valor de un campo fluctúa
alrededor de un valor determinado y constante. Aún el vacío perfecto a temperatura
de cero absoluto posee campos fluctuantes conocidos como "fluctuaciones del vacío",
una energía que corresponde a la mitad de la energía de un fotón.
Las fluctuaciones del vacío, aunque lo parezcan, no son abstracciones en
la mente de un físico. Tienen consecuencias observables que se pueden visualizar
directamente en experimentos a escala microscópica. Por ejemplo, un átomo que ha
sido llevado a un estado de excitación no permanece así para siempre, sino que
vuelve a su estado normal espontáneamente, emitiendo un fotón. Este fenómeno
es una de las consecuencias de las fluctuaciones del vacío. Imagine que
mantiene un lápiz parado sobre su punta en el extremo de un dedo. Una vez
logrado el equilibrio, el lápiz se mantendrá en posición si la mano está
perfectamente estable y nada perturba
esa estabilidad. Pero la más mínima perturbación hará que el lápiz caiga para
adoptar una posición de equilibrio más estable. De manera similar, las
fluctuaciones del vacío llevan a que los átomos en estado excitado vuelvan
a su estado normal.
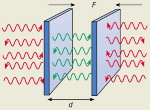
FIGURA 1
|
|
La Fuerza de Casimir es el efecto mecánico más famoso de las fluctuaciones del
vacío. Consideremos la separación entre los dos espejos planos como una cavidad
[Fig. 1]. Todos los campos electromagnéticos tienen un
"espectro" que los caracteriza, que contiene diferentes frecuencias. En el vacío
abierto todas las frecuencias tienen igual importancia, pero dentro de una cavidad,
donde el campo es reflejado una y otra vez entre los espejos, la situación es
diferente. El campo es amplificado en múltiplos enteros de la mitad de la
longitud de onda que cabe justo dentro de la cavidad. Esta longitud de onda corresponde
la "resonancia de cavidad". A otras longitudes de onda, en contraste, el campo
resulta suprimido. Las fluctuaciones del vacío son suprimidas o amplificadas
dependiendo de que sus frecuencias correspondan o no a la resonancia de la
cavidad.
Una cantidad física importante cuando se habla de la Fuerza de Casimir es la
"presión de radiación del campo". Todo campo —incluyendo el campo del
vacío— tiene una energía. Como todos los campos electromagnéticos se pueden
propagar por el espacio producen presión en las superficies, del mismo modo que
un río que circula empuja sobre una represa. Esta presión de radiación crece
con la energía —o sea con la frecuencia— del campo electromagnético.
A la frecuencia de resonancia de la cavidad, la presión de radiación dentro de
la cavidad es mayor que fuera de ella y entonces los espejos son empujados
hacia fuera. Fuera de resonancia, en cambio, la presión de radiación dentro
de la cavidad es más pequeña que la de afuera.
El resultado es que, luego producirse el adecuado balance de fuerzas, los
componentes de atracción son un poco más fuertes que los de repulsión, debido
al simple hecho de que parte del campo no puede producir efecto dentro de la
cavidad por estar fuera de resonancia, mientras que en el exterior actúan todas
las frecuencias libremente. Para dos espejos perfectos y planos la Fuerza de
Casimir, en consecuencia, es de atracción, de modo que los espejos son
empujados uno contra el otro. La fuerza (F) es proporcional al área
(A) de los espejos y varía en proporción inversa a la distancia
(d) entre ellos: F ~ A / d4.
Aparte de los parámetros geométricos, la fuerza sólo depende de valores
fundamentales: la constante de Planck y la velocidad de la luz.
Aunque la Fuerza de Casimir es muy pequeña como para observarla en espejos
separados por metros o centímetros de distancia, sí es posible medirla en
espejos ubicados a micrones uno del otro. Por ejemplo, dos espejos con un
área de 1 cm2 separados por una distancia de 1 µm reciben
una fuerza atractiva de Casimir de alrededor de 10-7 N, un
valor cercano al peso de una gota de agua de medio milímetro de diámetro.
Aunque el valor pueda parecer pequeño, a distancias de menos de un micrómetro
la Fuerza de Casimir es la más fuerte que se puede producir entre dos
objetos neutros. A separaciones de 10 nm, alrededor de cien veces
el tamaño típico de un átomo, el Efecto Casimir produce fuerzas equivalentes
a una atmósfera de presión.
Aunque nosotros no tenemos una relación cotidiana con distancias así,
éstas son importantes en estructuras a nanoescala y en los sistemas
microelectromecánicos (MEMS). Se trata de artefactos de tamaños micrométrico
en los que las partes fijas y móviles, como pequeños sensores y actuadores,
se excavan en un sustrato de silicio. Luego se conectan equipos electrónicos
a este microartefacto para procesar la información que él mide o para gobernar
el movimiento de sus partes. Los MEMS tienen muchas aplicaciones potenciales en
la ciencia e ingeniería, y ya se los usa como sensores de presión en los
sistemas de protección para accidentes de auto que comercialmente se llaman
"air-bag".

FIGURA 2
|
|
Como los MEMS se fabrican a escala de micrones y submicrones, la Fuerza de Casimir
puede hacer que las pequeñas partes móviles se "peguen" entre sí, como fue reportado
hace poco por Michael Roukes y sus compañeros del California Institute of Technology
(1).
Pero es posible dar un buen uso a la
Fuerza de Casimir. El año pasado Federico Capasso y su grupo de Lucent Technologies
mostraron cómo se puede usar para controlar el movimiento mecánico de un MEMS
(2). El
investigador suspendió una placa de polisilicon
de un eje de torsión, una barra horizontal de unos pocos micrones de
diámetro [Fig. 2]. Cuando acercó una esfera metalizada
a la placa, la fuerza de atracción de Casimir ejercida entre los dos objetos
la hizo rotar. Haciendo oscilar la placa, el equipo analizó además el comportamiento
dinámico del MEMS. La Fuerza de Casimir redujo el ritmo de oscilación y el experimento
exhibió fenómenos no lineales, como histéresis y biestabilidad en la frecuencia de
respuesta del oscilador. De acuerdo con el equipo de investigación, el comportamiento
del sistema cumplió las previsiones que se habían calculado teóricamente.
Midiendo el Efecto Casimir
Cuando se predijo el Efecto Casimir en 1948 era muy difícil medirlo con el
equipamiento disponible en esa época. Uno de los primeros experimentos lo realizó
Marcus Spaarnay en 1958 en la Philips de Eindhoven, cuando investigaba la Fuerza de
Casimir entre espejos metálicos fabricados de aluminio, cromo o acero. Spaarnay
midió la fuerza utilizando una balanza de resortes y monitoreando la capacitancia
de las placas. Para evitar que la Fuerza de Casimir fuera modificada por fuerzas
electrostáticas, antes de hacer la medición debían descargar los espejos cerrando
circuito entre ellos. Además, Spaarnay debía asegurarse de que las caras de
los espejos estuvieran perfectamente paralelas entre sí, ya que la Fuerza de
Casimir es extremadamente sensible a los cambios de distancia. Spaarnay
hizo todo lo posible para superar estas dificultades y concluyó que sus resultados
"no contradecían la predicción teórica de Casimir".
Ahora hay sofisticados equipos que han permitido estudiar mucho mejor el Efecto
Casimir. La nueva generación de mediciones comenzó en 1997. Steve Lamoreaux,
de la Universidad de Washington en Seattle, EE.UU., midió la Fuerza de Casimir
entre un lente esférico y una placa de cuarzo, ambos cubiertos
por una capa de cobre y oro. El lente y la
placa estaban conectados a un péndulo de torsión —una barra horizontal de
torsión suspendida de un alambre de tungsteno— colocado dentro de un
recipiente cilíndrico al vacío. Cuando Lamoreaux acercó la lente y la placa
hasta ponerlos a unos micrones de distancia, la Fuerza de Casimir acercó los
objetos y causó un cambio en el recorrido del péndulo. Con este experimento
encontró que las mediciones coincidían con los valores previstos por la
teoría con una precisión del 5%.

FIGURA 3
|
|
Inspirados por el avance de Lamoreaux, otros investigadores probaron otras
formas de medir el Efecto Casimir. Umar Mohideen y sus compañeros de la Universidad
de California en Riverside, EE.UU., por ejemplo, sujetaron una esfera de poliestireno
de 200 µm de diámetro a la punta de medición de un microscopio de fuerza
atómica [Fig. 3]. En una serie de experimentos acercaron
la esfera, cubierta a veces de aluminio y otras de oro, a alrededor de 0,1 µm
de un disco plano, también cubierto de esos metales. La atracción resultante entre
la esfera y el disco fue monitoreada por la desviación de un haz de láser. Los
investigadores lograron mediciones de la Fuerza de Casimir dentro del 1% de los
valores esperados teóricamente.
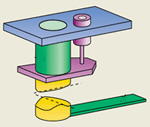
FIGURA 4
|
|
Thomas Ederth, del Royal Institute of Technology de Stockholm, Suecia,
utilizó también un microscopio de fuerza atómica para estudiar el
Efecto Casimir. Midió la fuerza entre dos cilindros cubiertos de oro
colocados a 90° uno del otro a una distancia de apenas 20 nm.
Los resultados que obtuvo coinciden con la teoría con sólo 1% de
variación [Fig. 4].
Muy pocos experimentos recientes han medido la Fuerza de
Casimir utilizando la disposición original de dos espejos planos,
paralelos entre sí. La razón es que se debe mantener los espejos
perfectamente paralelos durante el experimento y esto es difícil
de lograr. Es mucho más fácil colocar una esfera cerca de un espejo
debido a que la separación entre ambos objetos es, simplemente, la
distancia más corta entre ellos. El único problema al usar una esfera
es que los resultados de los cálculos de la Fuerza de Casimir no son
tan exactos como cuando se usan espejos planos. Particularmente, se
ha debido asumir que las contribuciones a la fuerza entre la esfera
y la placa en cada punto son completamente independientes. Esto es
cierto sólo si el radio de la esfera es mucho mayor que la distancia
entre ella y la placa.
El único experimento reciente que ha reproducido la distribución
original de Casimir de dos espejos planos paralelos fue realizado
por Gianni Carugno, Roberto Onofrio y otros de la Universidad de
Padua en Italia, quienes midieron la fuerza entre una placa rígida
cubierta de cromo y la superficie de una placa móvil hecha del
mismo material, separadas por distancias entre
0,5-3 µm (3).
Los investigadores hallaron que la Fuerza de Casimir medida estaba
dentro del 15% de los valores teóricos esperados. Esta aproximación
tan pobre refleja las dificultades técnicas que involucró el
experimento.
Mejores cálculos
Cuando se estudia el Efecto Casimir, el problema es que los espejos
reales no se parecen en nada a la superficie lisa y perfectamente
plana que consideró Hendrik Casimir originalmente. En particular,
los espejos reales no reflejan todas las frecuencias a la perfección,
sino que lo hacen bien con unas y muy mal con otras. Además,
todos los espejos se vuelven transparentes a las frecuencias
muy altas. Para calcular la Fuerza de Casimir se debe tener en
cuenta coeficientes de reflexión de los espejos que dependen de la
frecuencia, un problema que abordó por primera vez Evgeny Lifshitz
a mediados de los 50s y luego Julian Schwinger y otros.
Resulta ser que la medición de la Fuerza de Casimir entre espejos
metálicos reales ubicados a 0,1 µm de distancia es de sólo
la mitad del valor predicho teóricamente para espejos perfectos.
Si no se tiene en cuenta esta discrepancia cuando se comparan los
datos experimentales con teóricos, las mediciones experimentales
pueden ser interpretadas erróneamente como nuevas fuerzas.
Astrid Lambrecht y Serge Reynaud, del Laboratoire Kastler Brossel,
Université Pierre et Marie Curie, tomaron en consideración en
sus cálculos el comportamiento real de los espejos, teniendo en
cuenta las propiedades físicas de los metales. Encontraron que los
modelos simples de espejo de estado sólido sólo cumplen con el
comportamiento real a separaciones mayores de 0,5 µm.
Otro problema del cálculo de la Fuerza de Casimir que se debe
esperar en un sistema real es el hecho de que los experimentos
nunca se realizan al cero absoluto —como fue definido
originalmente en los cálculos de Casimir— sino a temperatura
ambiente. Esto causa que —además de las del vacío— entren
en juego las fluctuaciones térmicas. Estas fluctuaciones térmicas
pueden producir su propia presión de radiación y crear una
Fuerza de Casimir mayor a la esperada. Por ejemplo, la Fuerza de
Casimir entre dos espejos planos a 7 µm uno de otro es el
doble a temperatura ambiente que al cero absoluto. Afortunadamente,
las fluctuaciones térmicas a temperatura ambiente sólo son
importantes si la separación es de más de 1 µm, ya que con
una distancia menor la longitud de onda de las fluctuaciones
térmicas es demasiado grande para entrar en la cavidad.
Aunque la dependencia a la temperatura de la Fuerza de Casimir
aún no ha sido estudiada en detalle experimentalmente, debe ser
incluida en los cálculos de la fuerza en separaciones mayores de
1 µm. Muchos investigadores han abordado el cálculo en
espejos de reflexión perfecta, incluyendo a Lifshitz y Schwinger
en los 50s. El tema fue examinado más recientemente por Michael
Bordag en la Leipzig University, Bo Sernelius en la Linköping
University de Suecia, Galina Klimchitskaya y Vladimir Mostepanenko
en la Universidad de Paraiba en Brasil y por Astrid Lambrecht y
Serge Reynaud, del Laboratoire Kastler Brossel, Université Pierre
et Marie Curie, de París, Francia. La dependencia de la temperatura
de la Fuerza de Casimir ha sido causa de fuertes debates en la
comunidad científica. Varias de las contradicciones que presentaba
la discusión se han ido resolviendo, lo cual ha dado un motivo
adicional para que se realice una observación experimental de la
influencia de la temperatura en la Fuerza de Casimir.
El tercer y definitivo problema en el cálculo de la Fuerza de
Casimir es que los espejos reales no son perfectamente lisos.
La mayoría están hechos con una base cubierta de una capa
delgada de metal, aplicada por una técnica llamada "sputtering"
("escupida"). Sin embargo, este proceso produce capas con
rugosidades de 50 nm. Aunque esta rugosidad es invisible al
ojo desnudo, afecta enormemente las mediciones de la Fuerza de
Casimir, que es muy sensible a los pequeños cambios en la
distancia.
Mohideen y su grupo de California han usado recientemente
deformaciones de superficie para demostrar que dos superficies
pueden recibir fuerzas laterales de Casimir que actúan en
sentido paralelo —en lugar de perpendicular— a la
superficie de los espejos. En ese experimento prepararon espejos
especialmente corrugados en forma sinusoidal. Movieron los
espejos manteniéndolos paralelos entre sí de modo que los
"picos" del corrugado de un espejo pasaran sucesivamente
sobre los picos y valles del otro. Encontraron que la fuerza
lateral de Casimir varía sinusoidalmente con la diferencia de
fase entre las dos formas corrugadas. El tamaño de la fuerza
es alrededor de diez veces menor que la fuerza ordinaria de
Casimir entre dos espejos ubicados a la misma distancia. La
fuerza lateral también se debe a las fluctuaciones del vacío.
Mehran Kadar y sus colegas del Massachusetts Institute of
Technology (MIT) de EE.UU. han calculado un valor teórico de
la fuerza lateral entre dos espejos corrugados de reflexión
perfecta. Mohideen y sus colegas evaluaron la fuerza lateral
para espejos metálicos, encontrando que los valores coinciden
bastante bien con los del experimento. La fuerza lateral de
Casimir puede tener consecuencias en las micromáquinas.
¿Una nueva física?
El Efecto Casimir puede jugar, además, un rol en la medición precisa
de fuerzas en escalas de nanómetros y micrómetros. La ley del
cuadrado inverso de la gravitación de Newton ha sido probada varias
veces en distancias macroscópicas al observar el movimiento de los
planetas. Paro nadie ha logrado verificar esta ley con precisión a
escala del micrón. Tales pruebas son importantes debido a que muchos
modelos teóricos que intentan unificar las cuatro fuerzas fundamentales
de la naturaleza predicen la existencia de fuerzas desconocidas que
actúan a tales escalas. Cualquier desviación entre la teoría y los
resultados experimentales puede sugerir la existencia de nuevas
fuerzas. Pero no está todo perdido cuando los valores coinciden,
ya que las mediciones pueden establecer nuevos límites a las
teorías existentes.
Jens Gundlach y sus colegas de Washington, por ejemplo, han usado
un péndulo de torsión para determinar la fuerza gravitacional
entre dos masas de prueba separadas por distancias entre 10 mm y
220 µm. Sus mediciones confirman que la gravitación newtoniana
opera en estas escalas, pero la Fuerza de Casimir domina a distancias
menores. Joshua Long, John Price y colegas de la University of
Colorado —junto a Ephraim Fischbach y colegas de la Purdue
University— están intentando eliminar el efecto Casimir
en sus pruebas de gravitación a escalas menores a un milímetro
eligiendo con mucho cuidado los materiales que utilizan en el
experimento.
Hasta ahora hemos tenido un panorama de los diversos experimentos
y estudios teóricos relacionados con el Efecto Casimir. Hay varias
investigaciones más que resultan excitantes. Por ejemplo, varios
grupos han estado observando qué ocurre si la interacción entre
dos espejos no es producida por un campo electromagnético —que
está formado por bosones sin masa— sino por masivos fermiones,
tales como los quarks y los neutrinos. Otros grupos de investigación
están estudiando el Efecto Casimir en diferentes topologías, tales
como cintas de Möebius y objetos toroidales (en forma de
rosquilla).
Pero a pesar de los intensos esfuerzos de los investigadores de este
campo, quedan varios problemas sin resolver en el tema del
Efecto Casimir. En particular la aparentemente inocente cuestión
de la fuerza de Casimir dentro de una esfera hueca, que sigue
siendo materia de un vivo debate. La gente no está segura de si
la fuerza es atractiva o repulsiva. El propio Hendrik Casimir
meditó sobre este problema en 1953 mientras buscaba un modelo
estable para el electrón. Medio siglo después, los misterios de
la Fuerza de Casimir parecen suficientes para mantener entretenidos
a los equipos de investigación por varios años más.