Topólogos predicen una nueva forma de materia

Una conexión entre la mecánica cuántica y la topología implica la existencia de un estado enteramente nuevo de la materia. Y los físicos ya han encontrado el primer ejemplo

En 1970, un joven físico trabajando en la Unión Soviética presentó una predicción que contradecía la intuición. Vitaly Efimov, en la Universidad de Washington, Estados Unidos, en este momento, demostró que los objetos cuánticos que no se pueden formar en pares podían, sin embargo, formar tripletes.

En 2006, un grupo austríaco halló el primer ejemplo del llamado «estado de Efimov» en un gas frío de átomos de cesio.

Es desconcertante. Con seguridad, los enlaces que unen los tripletes son los mismos que unen los pares. ¡Pero en realidad no!
Resulta que existe una diferencia sutil pero importante que hace que estos enlaces sean completamente diferentes.

Nils Baas, de la Universidad Noruega de Ciencia y Tecnología, hace ahora otra asombrosa predicción. Dice que los extraños enlaces como del más allá que permiten que los átomos de cesio se unan en tripletes deben permitir que se formen también objetos mucho más complejos. De hecho, dice que estamos a punto de descubrir una nueva forma de materia regida por una rama completamente nueva de la física.

Tras este extraño resultado está la rama de las matemáticas que se conoce como topología, el estudio de las formas. La topología se refiere en particular a las propiedades de las formas que se conservan cuando un objeto se comprime, estira y deforma, sin llegar a romperse.

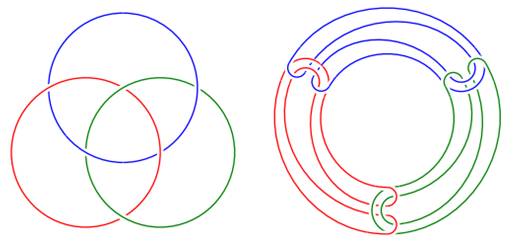
Un útil ejemplo es considerar el famoso anillo Borromeano que se ve en la imagen, arriba a la izquierda. Consiste de tres círculos entrelazados de tal forma que al cortar uno se liberan los otros dos.

Un punto clave aquí es que los círculos sobre un plano de dos dimensiones no pueden formar un anillo Borromeano. Pero al introducir una tercera dimensión, de repente todos los círculos se pueden vincular de esta forma. Por supuesto, cualquier planilandense viviendo en ese mundo de 2D quedaría completamente desconcertado por esa propiedad.

Resulta que hay una analogía matemática formal entre el anillo Borromeano y los extraños tripletes de cesio que predijo Efimov. Las matemáticas de la mecánica cuántica y la topología pasan a ser las mismas.

Pero aquí está el tema: los enlaces que emergen de la topología de la mecánica cuántica son por completo fuera de este mundo. Si bien la materia común, la materia sobre la que uno puede golpear con los nudillos, claramente está confinada en tres dimensiones, las matemáticas de la mecánica cuántica existen en un conjunto completamente distinto de dimensiones. Y es en este espacio en el que se forman los anillos Borromeanos.

El resultado es una especie de física paralela, en la que las leyes que gobiernan el comportamiento de este universo paralelo ejercen una tracción fantasmal e ineludible sobre nuestro universo.

Y no son sólo los enlaces entre átomos los que se ven afectados. Los físicos están empezando a construir conductores y aislantes en los que el movimiento de los electrones es gobernado por la topología de la mecánica cuántica. Los que se conocen como aislantes topológicos son un tema crucial y de actualidad en la física de estado sólido.

Y la topología está por extender su influencia, si Baas está en lo cierto. Él señala que los anillos Borromeanos son el ejemplo más simple de una tabla periódica completa de estructuras topológicas. Y si es posible crear estados de Efimov equivalentes a los anillos Borromeanos, entonces debería ser posible hacer otros, también.

Esta familia de vosas sería un nuevo estado de la materia regido por nuevas reglas, una especie de “física de Efimov”. ¿Cómo se comportaría esta materia? No está claro aún, pero Baas presenta una interesante posibilidad. El profundo y extraño vínculo entre partículas en los estados de Efimov es notablemente similar al entrelazamiento cuántico.

Nadie está muy seguro de si son idénticos, pero si lo son, la física de Efimov nos aportará una nueva forma de pensar sobre el entrelazamiento y sobre cómo generarlo y aprovecharlo. Esto tendrá importantes implicaciones para la criptografía, la computación y la ciencia de la información en general.

El ganador del Premio Nobel de Física Murray Gell-Mann afirmó en una ocasión que: “Todo lo que no está prohibido, es obligatorio”. Se refería a la forma en que interactúan las partículas en la mecánica cuántica. En otras palabras, si no hay una razón por la que las partículas no puedan interactuar de cierta forma, entonces deben interactuar de dicha manera.

Parece que vamos a poder ver cuán profunda es esta afirmación y qué alcance puede tener.

Fuente: Technology Review. Aportado por Eduardo J. Carletti


Más información: